Abstract
The internal Church thesis (𝗖𝗧) is a logical principle stating that one can associate to any function f : ℕ → ℕ a concrete code, in some Turing-complete language, that computes f. While the compatibility of 𝗖𝗧 in simpler systems has been long known, its compatibility with dependent type theory is still an open question. In this paper, we answer this question positively. We define “𝗠𝗟𝗧𝗧”, a type theory extending 𝗠𝗟𝗧𝗧 with quote operators in which 𝗖𝗧 is derivable. We furthermore prove that “𝗠𝗟𝗧𝗧” is consistent, strongly normalizing, and enjoys canonicity using a rather standard logical relation model. All the results in this paper have been mechanized in Coq.a
1. Introduction
“Calculemus!” With this word, Leibniz famously enjoined the reader to compute. Contemporary logicians took this motto as a founding principle after the progressive discovery of the proof-as-program correspondence. This major breakthrough, also known as the Curry-Howard equivalence, is the seemingly simple observation that proofs and programs are the same object, in an essential way.
One major offshoot of the Curry-Howard philosophical stance is Martin-Löf’s type theory (MLTT), the theoretical underpinning of several widely used proof assistants such as Agda, Coq, or Lean.16 In these systems, there is no formal separation between proofs and programs, as they live in the same syntax and obey the same rules. This monistic credo turns MLTT into the quintessential intuitionistic foundation of our modern times, blending logic and computation into the very same cast. Moreover, in the wake of the Swedish tradition of neutrality, MLTT does not pick a side in the constructivist feud. It neither proves fan principles from the Brouwerian band nor mechanistic axioms from the Markovian clique, and adheres to a strict Bishopian minimalism. If set theory is the paradise of mathematics, then type theory truly is the paradise of constructive mathematics.
Meanwhile, on the other side of the iron curtain, the Russian constructivists led by Markov pushed the computability tenet to an extreme point, postulating that all mathematical objects were indeed algorithms. Their doctrine15 is materialized by a foundational system that can be summarily described as a neutral Bishop intuitionistic logic extended with two additional axioms: Markov’s principle (MP) and Church’s thesis (CT).23
Of those two axioms, Markov’s principle is the simplest to state, as it is pretty much self-contained:
Common alternative formulations include “a Turing machine that does not loop terminates” or “non-zero reals are apart from zero”. is a sweet spot of semi-classical logic, as it can be given a computational content preserving the witness property.7
Church’s thesis is somewhat more involved, as it requires the internal definition of a computation model in the logic itself. Assuming a logic rich enough, this is traditionally13 achieved by defining the decidable Kleene predicate and its associated primitive recursive decoding function . Assuming to be the syntactic code of some program in the chosen Turing-complete computation model, some integer argument, and some encoding of evaluation traces of the model, then holds whenever is the trace of the fact that applied to evaluates to some integer . Furthermore, if indeed the predicate holds, then should return the value .
Assuming we have settled this computational paraphernalia, is simply the internal statement
Said otherwise, any function definable in the theory is known to be computable by some concrete algorithm from within the theory.
Contrarily to , which is a consequence of excluded middle, is a very anti-classical axiom.23 Assuming very weak forms of choice, it contradicts lesser variants of excluded middle. Similarly, it disproves choice-like principles, such as double negation shift. Finally, it also makes the logic very intensional as it contradicts function extensionality, under the same kind of weak choice assumptions.
The consistency of and with regard to some logical system is typically proved via realizability, which is the intended model of the Russian dogma. Quite remarkably, Kleene’s seminal paper14 already proves that is compatible with Heyting’s arithmetic. For a more expressive theory, the effective topos is a famous example of a realizability topos in which both principles hold.10
Considering the claim above that in proofs are programs, it does seem a bit surprising that it is not biased toward the Russian school. Surely it ought to be easy to convert to the Markovian orthodoxy, for otherwise the Curry-Howard mantra would be but a misleading advertisement. Let us survey the current status of each Russian axiom individually in the canon of dependent type theory.
As we already hinted at, it is known that is not derivable in .4 Since it is a consequence of classical logic, it holds in classical models such as the set-theoretical one,25 but it is also possible to add to while retaining the computational properties through a form of delimited exceptions.19 Note that, due to the minimalism of , the alternative statements of mentioned previously are not equivalent in this setting.3
As for , we already stated that it is negated by classical models, and thus is not a consequence of . By contrast with , the compatibility of with dependent type theory is a much more contentious subject. To make things simpler, we will therefore focus on this single principle in this paper, and deliberately ignore Markov’s principle. The proviso about phrasing of the statement mattering a lot is even more paramount with , which is the chief reason why the problem and its answers are a matter of debate. In the remainder we will prove that is indeed compatible with the strongest form of Church’s thesis usually agreed upon, but for this we first need to explain what we actually mean by these sibylline words. We dedicate the next section to a thorough exegesis of this topic.
2. A Comprehensive Scan
Contrarily to more archaic systems, does not need a realizability interpretation to turn its proofs into programs. In some sense, it is already a realizability interpretation, as terms are literally bona fide programs. It should therefore be very natural to add to .
As a matter of fact, as long as the context is empty, the following rule is admissible
where is some term derived from in a systematic way. Depending on the pursued goal, this process is variously known in the type theory world as extraction18 or quotation.21 Obviously, a rule that is derivable for closed sequents is not necessarily internalizable in the theory, so there is a non-trivial gap to fill there.
An additional issue is that dependent type theories have various notions of existence. Typically, they contrast dependent sum types with existential types . The precise details depend on the exact theory considered, but the general rule is that the former corresponds to actual, constructive evidence, while the latter stands for mere existence—that is, no computational content can be extracted from this type. Such non-computational types are called propositions, an umbrella term for mildly related concepts. The three most common instances of propositions are captured by the realizability-driven universe of ,18 the subuniverse inspired by the univalent world,24 and the universe of strict propositions.6 Regardless of the setting, -types validate choice by construction through large elimination or projections, while existential types do not, in general.
The arithmetic statement of mentions two existential quantifiers, hence we have a priori at least four possible translations into . In practice, the second one returns an enumerable proposition, so that for most notions of proposition, namely with singleton elimination or with unique choice, the use of or results in equivalent statements. We will thus always stick to a -type for this quantifier. More problematic is the first existential quantifier, the nature of which leads to radically different worlds. We will call (resp. ) the statement of Church’s thesis with a (resp. ) type as the first existential quantifier.
As mere existence does not validate choice by default, is much closer to the traditional first-order setting. When is taken to live in the universe of , the relative expressivity of has been studied extensively in the setting of synthetic computatibility.5 An important remark is that the lack of choice prevents building an internal quoting function that associates to some function its concrete code. As already suggested before, this means that does not necessarily contradict function extensionality. Actually, we can even go much further: In the case where propositions are identified with s, turns out to be compatible not only with but also with full-blown univalence.22 More generally and quite counterintuitively, univalence is compatible with many principles that would make the hardcore Bishop-style intuitionist raise a suspicious eyebrow, as long as they are squashed enough and thus made computationally harmless.22,24
Contrastingly, as -types come with intuitionistic (non)-choice built-in, is the telltale of an extremely weird mathematical realm. For starters, it immediately implies the existence of a quoting function and breaks both function extensionality and classical logic. The consistency of with is an open problem that has been lingering for a while and seems to be considered a difficult question by experts.11,22 The best result thus far is the consistency of with a stripped-down version of without the so-called rule:
The model used to prove this fact is a variant of Kleene realizability tailored for dependent types. Briefly, in this model, terms are interpreted directly as their code in Kleene’s first algebra, that is, a natural number, and the equational theory in a context is defined as the closure of code equality by ground substitutions.
This representation makes the implementation of trivial, as it boils down to the identity. Yet, for this to work, it is critical that two functions convertible in the model have literally the same code. This is exactly where the restriction to ground substitutions comes into play, as it will identify functions with their concrete syntax. Unfortunately, the same restriction also destroys non-trivial higher-order equations and in particular invalidates the rule.
Although we understand the difficulties experienced by the authors of this paper and acknowledge their distinct goals, we consider that removing this congruence from when precisely trying to implement a principle implying the existence of a quoting function is unarguably throwing the baby with the bath water. Ubiquitary conversion under -abstractions is a stepping stone of for program reasoning, so treating functions as black boxes is a no-go and the rule a sine qua non.
Given the strong relationship between quoting functions and metaprogramming, we should also mention some attempts at making the latter a first-class citizen of dependent type theory. These systems are built with practical programming in mind rather than constructive mathematics, but the endeavours are similar enough that they are worth highlighting. There is in particular a wealth of literature on contextual types,17 a special kind of modal type8 capturing well-typed terms in an object context. Although contextual types can coexist with dependent types, the ability to pattern-match on code in these settings is still a difficult problem that is only satisfyingly handled in the absence of dependent types.12
3. High-Level Description
We now give the high-level intuitions that we develop technically later on. In this paper, we define , read “ with quotes”, a minute extension of with quoting operators that implement in a straightforward way. As already explained, holds externally in . If we want it as an internal rule, there are two problems to solve: first, handling terms in an arbitrary context, and second, showing that our hypothetical internalization preserves conversion.
Despite the aura of complexity surrounding this question, our solution is disappointingly simple. The first problem will be handled in the most trivial way one can think of. Namely, the primitives computing the internal version of will simply block as long as their arguments are not closed. Since the return type of these primitives is first-order, this will not be a problem as it will not endanger canonicity.
The second problem is solved in a similarly obvious manner. Given two terms one needs to ensure that the quotation of these terms agree. In particular, the integer code returned by these operations must be the same. This sounds complicated, as in general two equivalent functions may have different codes. In Turing-complete languages, this is actually impossible to achieve in a computable way, due to Rice’s theorem. But in , there is a very simple way to find a canonical representative of an equivalence class of functions: ust pick the normal form! Conversion in is decidable, as it virtually amounts to comparing the normal forms of the considered terms for syntactic equality. This requires that all well-typed terms have a normal form, but this property is usually taken for granted in dependent type theories and will for sure hold true in .
As the astute reader may complain about, this is not enough in presence of -rules, which are included in our system. But even in this case, our normalization trick can be adapted simply by maximally -reducing and stripping and pair annotations from the normal form.
Despite the intuitive simplicity of the above guiding ideas, proofs about dependent type theory are very tedious and error-prone, let alone when they contain bits of computability. To keep the naysayer at bay, all proofs were mechanized in the Coq proof assistant.
4. Basic Type Theory
Let us fix some conventions. Since we will be juggling quite a bit between levels, we will use a different font style to refer to objects from the metatheory, with types in and type ascription written in set-theoretic style . Some metatheoretical types of interest are , the metafunctions from to , and the metaintegers. We will write for the type of terms defined later on.
Our base theory will be an instance of featuring one Russell-style universe, negative and types with definitional -rules, together with a natural number type, an empty type and an identity type. We recall the syntax of this theory in Figure 1. The typing rules are standard and we let the reader refer to the mechanization for details.
We use the usual notations and for non-dependent product and sum. We write for when is clear from the context. Similarly, we sometimes drop the annotations of -abstrations and pairs. If , we write for the unary numeral associated to . We write for numbers intended to code for programs.
Partial computations are usually defined through the partiality monad . Since we will only ever consider partial integers, we use a simpler encoding.
We define the type of partial integers . The intuitive meaning of a partial integer is the following.
If for all , , then is undefined.
Otherwise, let be the smallest integer such that for some . Then evaluates to .
This can be easily internalized in .
Given , and , we define the step-evaluation predicate.
read “ evaluates to in steps” by recursion on , that captures the above intuition. Most notably if , is convertible to
Given the algorithmically friendly nature of , we will pick a slightly nicer, but equivalent, phrasing of . We will merge the Kleene predicate and its decoding function into a single function .
Henceforth, we will define in as
for some term .
5. Extensions
We now turn to the definition of the extensions that define proper.
The new term constructors of are defined in Figure 2, and will be collectively referred to as the quoting primitives.
We give names exposing the intuition of the meaning of those terms. The term is the quote of , which is intended to return the code of the function . The term is the step-count of applied to —that is, it will return the number of steps needed to evaluate the quote of on argument . Finally, is the reflection of applied to , which produces a proof that indeed the quote of fullfils the expected runtime behavior.
A computation model for is given by a metafunction and an internal evaluation function .
To define the typing system alone we do not need any additional requirements on those objects, but let us offer some intuition before proceeding any further.
The function is just some arbitrary Gödel numbering of the syntax. As already explained, the function is going to serve as a Kleene predicate expressed in a functional form. In particular, we expect and to compute the result of the application of the program to the argument if it exists. In practice, is expected to be defined in alone, or for that matter, in a much weaker fragment corresponding to . In the remainder of this paper, we assume a fixed computation model.
We write
for the specification of the quoting operators on and . Furthermore, given any , let
We now have enough to define the typing rules of the additional primitives in Figure 3. We delay the description of the conversion rules of these primitives to a later point, because we still need more infrastructure.
Still, these rules are enough for the following theorem.
proves.
The types are just the Skolemization of .
To finish the specification of , we need to define its conversion rules. This requires some heavy definitions.
Given and , we say that is -quasi-closed, written if, ignoring and pair annotations, all free variables of are in . When is empty, we will write .
We recall the inductive definition of deep normal and neutral forms of terms at Figure 4 and define the additional rules for at Figure 5.
Normal forms are, as usual, terms which cannot be simplified further. Neutral forms are a subcase of the former, intuitively capturing the notion of a term whose evaluation is blocked due to a variable not bound to a value. In particular, they cannot trigger new conversions when they are substituted for a variable. Our definition is standard for the fragment, except maybe that we we ignore and pair type annotations just like for the predicate. Only worth discussing are the newly introduced terms of .
The quote primitives do not generate any new non-neutral normal forms, as their types are concrete, canonical datatypes. They do generate new neutrals, though. The intuition is that these primitives only compute on closed normal forms, so if one of their argument is not closed, they will block and thus be neutral.
We write if both and .
The last non-trivial ingredient that is needed is erasure of terms. We rely on it to quotient normal forms with regard to the various -rules of our system.
Given , we define its erasure . This operation can be understood as the composition of two finer-grained primitives: first, replace and pair type annotations with a dummy term, and second, perform maximal -reduction of and pair nodes. We choose for the dummy term, but any closed normal term would do. We give the relevant operations in Figure 6, all other cases are term homomorphisms.
If , we write .
Given we define by induction on as
We now have all the necessary definitions to define the new conversion rules of at Figure 7. We omit the obvious congruence rules, and we give some intuitions by paraphrasing the rules. The computation rule for is simply stating that quoting a closed normal term produces the Gödel number of its erasure. The two other rules reflect the behavior of the operator in the theory itself. They start by assuming that is a closed normal term, so its quote is a concrete code. Assuming canonicity, for any , must be convertible to a numeral. Similarly, must be convertible to some numeral .
Since we expect to model the computation of , there must be some smallest s.t. is convertible to . Then returns , and must provide a closed proof of . But given the previous assumptions, is convertible to a finite sequence of products of equalities with a trailing equality . This type is trivially inhabited by .
6. Adequacy and Soundness
There is still one missing piece for to make sense. Indeed, in the intuitive explanation above, we argued that should model the runtime behavior of . In spite of this, we have made no additional assumption on Definition 5 so far. We make this requirement formal as computational adequacy in this section. This first forces us to endow with a notion of evaluation.
We define in the metatheory a step-indexed evaluation function that computes the deep normal form. We omit the standard rules for the fragment, and give them for extensions in Figure 8.
Although we describe it using inference rules, evaluation really is a step-indexed recursive function in the metatheory, of type . We write when it returns . We write when there exists s.t. .
We discuss briefly the evaluation rules for the quoting primitives. They start by deeply evaluating the subterms and checking whether they are quasi-closed. If not, they immediately return. Otherwise, they perform a macroscopic evaluation step. For , that just means quoting the closed normal form into a number. For and , it performs a guarded -recursion to find the smallest index such that the erasure of evaluates to a numeral.
We say that the computation model is adequate if it satisfies the following:
We have a derivation .
For all and ,
if then ,
if then .
The last point is essentially stating that the metatheoretical evaluation and the internal evaluation coincide.
From now on, we implicitly assume that our globally fixed computational model is adequate. The remainder of the paper is dedicated to the proof of the following theorem.
is consistent and strongly normalizing. Furthermore, any closed term normalizes to a numeral.
7. A Logical Relation Primer
We will prove Theorem 16 using a logical relation model. The base model is basically the now famous inductive-recursive one from Abel et al.,1 with a handful of surprisingly minor tweaks. In this section, we briefly recall the principles of Abel-style logical relations.
From a high-level point of view, Abel-style logical relations for are just a glorified kind of realizability with a lot of bells and whistles. Notably, in the semantic world, well-formed types are defined inductively, while well-typed terms are defined recursively over a proof . In turn, well-typedness is extremely similar to, say, Kleene realizability,23 that is, essentially means that weak-head normalizes to some value , further satisfying some conditions depending on . Due to conversion being an integral part of typing, one also needs to provide predicates for type and term convertibility at some semantic type.
The major departure from usual realizability in this kind of model is the proper handling of variables. All semantic predicates are actually presheaves over contexts equipped with weakenings. Furthermore neutral terms enjoy a very specific status; see, for example, Lemma 22. This will turn out to be important for our goals.
The relation itself is parameterized by syntactic predicates for the various notions of typing and reduction. These predicates must satisfy a list of closure properties, which are typically weaker than the ones enjoyed by the standard typing rules of . Another way to understand this is that logical relations turn a liberal type system, called declarative, with many closure rules that is easy to work with, into a lower-level type system that is hardly usable but which is similar in spirit to the steps performed by a typing algorithm. Proofs in this generic system are in some sense normalized compared to the declarative system. As a matter of fact, this is a way to prove decidability of type-checking, since an algorithmic presentation of type-checking will satisfy the low-level closure properties. A notable difference with the declarative system is that generic typing requires making explicit the notion of neutral terms, through the introduction of neutral convertibility, which can be understood as the usual convertibility restricted to neutral terms.
In the remainder of this section we assume fixed some instance of syntactic typing and reduction rules for . Due to their sheer size and the fact they are neither surprising nor new, we will not state the closure properties here, but rather refer to the corresponding Coq code.
A set of typing rules is generic when it enjoys a specific list of (weak) closure properties.
Given generic notions of typing and reduction, one can define reducibility in the abstract. Our base logical relation is unchanged with regard to Abel et al.,1 so we will not give the full definition here. To begin with, writing everything in full on paper would be both unreadable and uninformative, and probably ridden with typos. Rather, we sketch below some representative type formers to build intuition. We also ignore bookkeeping details that clutter the simplicity of logical relations, such as universe levels. Our results are backed up by a mechanized proof, so we can go for a fearless human-readable paper.
We give a partial but evocative definition of reducibility at Figure 9.
As already explained, we gloss over the details and instead concentrate on the high-level view. We abuse implicit arguments in Figure 9 to keep things readable, and we also omit additional well-formedness conditions. At the risk of repeating ourselves, this is really just the run-of-the-mill complete presheaf model for , where presheaves have been manually encoded by means of quantifications over all weakenings of the current context. Note the lack of naturality conditions thanks to Lemma 19. In our setting, typed reduction is simply untyped reduction annotated with proofs that both sides are well-typed and convertible. Similarly, well-typed neutrals are untyped neutrals together with a proof of well-typedness and self-convertibility. Without further consideration for the low-level details, the logical relation satisfies some salient properties that we list below.
For all proofs of type reducibility, ifthenand similarly for the other statements.
This allows us to silently drop the proof of type formation for reducibility statements as a notational device. As long as there is one, it does not matter which one we pick.
Ifthenand similarly for the other statements.
Reducibility is closed by typed anti-weak-reduction.
Well-typed neutrals are reducible.
Just like for standard realizability, we need to close reducibility by substitution to state the fundamental lemma. The relation resulting from this closure is known in the literature as validity. We refer to the development for reference.
Well-typed terms are valid.
8. The Logical Relation
For technical reasons, we will work with a slightly tweaked version of rules. Figure 7 is given for readability purposes; these rules will be derivable in the actual system. The differences are the following.
First, instead of a global typing axiom for , we add it as a premise to the rules for and . This is a cosmetic change to strengthen induction over derivations.
Second, for reasons that will become clear soon, we turn the well-typedness premises of those rules into self-convertibility. For instance, the introduction rule of becomes:
By reflexivity of term conversion, it is clear that these rules imply the ones from Figure 7. After Theorem 33, we will also be able to derive that self-convertibility implies well-typedness, which shows that the two versions are equivalent.
The model itself is defined in terms of a small-step reduction relation, so we need to define it properly for , in addition to the big-step variant from Section 6.
We mutually define weak-head and deep reductions, respectively written and . The rules are standard, and the rules are defined in Figure 10. Weak-head and deep reductions coincide for the quoting primitives.
Note that deep reduction is simply iterated weak-head reduction on the subterms of weak-head normal forms. Deep reduction is a specific sequentialization of evaluation, and its reflexive-transitive closure computes the same normal forms. Importantly, both reductions are deterministic.
One major remark for our proof to go through is that in Abel-style logical relations, the closure properties of conversion preserve deep normalization. Said otherwise, we never perform conversion on terms potentially introducing non-termination. We leverage this by the following decoration.
We define deep term conversion as the predicate extended with the following side-conditions.
For , there is some s.t. and .
and have the same erasure, that is, .
We define similarly deep-type and neutral conversions.
When instantiating the logical relation with deep conversions, one gets access to the fact that both sides of the conversion deeply normalize to terms that have the same erasure. This is why we turn the typing premises of the quoting primitives into self-convertibility. Before the fundamental lemma, syntactic deep self-convertibility gives more information than just syntactic typability.
The typing rules where the various conversion predicates are replaced by their deep equivalent satisfy the generic typing interface.
Note that erasing normal forms before comparing them is critical for the above lemma. Indeed, generic conversion rules for negative types are given directly as -expansions. Therefore, two convertible normal forms may differ on their annotations or up to some -expansion. Erasing all annotations and maximally -reducing ensures thus that the result is unique for each equivalence class.
As a result, the logical relation instantiated with deep typing is a model of . We only have to check that the additional rules are also interpreted. Since semantic self-convertibility is equivalent to semantic well-typedness, it is enough to check the rules from Figure 7, the ones from Figure 3 are a consequence of the former.
The conversion rules for theprimitive hold in the reducibility model.
We focus on the more general congruence rule. Assume , we now have to show that . By escape, . We thus have two terms and s.t. , and . Either both and are quasi-closed or both are not. In the latter case, both and are neutral and convertible, so by reflection they are reducibly convertible. Otherwise, they reduce to and , which are equal numerals and thus reducibly convertible. In either case we conclude by anti-reduction.
To prove reducibility of and , we need a fair amount of rewriting theory. The computation model is completely untyped, and we only care about erased terms, so we must consider reductions that ignore and pair annotations. The following are textbook results, except for the interleaving of weak and deep reduction for the quoting primitives.
We define parallel and standard reductions up toand pair annotations forin the usual way.
Parallel reduction is confluent.
Standard reduction to aimplies deep evaluation up to annotations, and is preserved by erasure.
We can now tackle the remaining reducibility proofs.
The conversion rules for the and primitives hold in the reducibility model.
The conversion rules for the and primitives hold in the reducibility model.
Once again we focus on the congruence rule. Since the two primitives behave computationally the same, we only treat the case which is more involved typingwise. Let us assume and . As before, we have deeply normal terms , (resp. and ) convertible to the original terms and with the same erasure, and thus the same closedness.
If not all these terms are closed, then and are convertible neutral terms, we conclude as above.
Otherwise, by reducibility, for some . Since reducibility is closed by application, we get . This implies that both applications deeply evaluate to the same semantic integer, that is, a series of successors ending either with or a neutral. By confluence, we rule out the second case as is closed, so these terms reduce to some numeral . By confluence and standardisation, also evaluates to . By irrelevance of erasure, also evaluates to . By computational adequacy, there exists some s.t. and for all . Given that and have the same erasure, this also holds for . Hence, and evaluate to and and evaluate to . The only remaining problem is to show that this value is indeed of semantic type . But this is a trivial consequence of the normalization properties of the terms implied.
Finally, one also has to prove validity for these conversion rules, that is, that they are stable by substitution. This turns out to be obvious. Congruence rules are stable by substitution by construction. For the other rules, it is enough to observe that both quasi-closedness and erasure of quasi-closed terms are stable by substitution. We thus get the result below, of which Theorem 16 is an immediate corollary.
Well-typed terms are valid.
9. Mechanization
While the Abel et al. proof has been implemented in Agda,1 our mechanization is written in Coq and is based upon a recent work by Adjedj et al.2 that relies on a small induction-recursion encoding.9 Apart from this, the two formalizations are globally the same. The only advantage of the Coq version, which we believe to be decisive, is the availability of tactics. The largish corpus of proofs relating the numerous untyped reductions is rendered tractable by careful automation.
All theorems stated in the paper have been formalized. The only thing that we did not formally prove was the actual existence of adequate models of computation. We globally axiomatized one in the development instead.
The reader may reasonably complain about the use of axioms, as they may very well be inconsistent. Yet, the existence of adequate models is at the same time an utterly trivial fact, and a technically extremely challenging task. Indeed, at an intuitive level has already been implemented in , because we defined evaluation as a step-indexed function in our metatheory, which turns out to be a variant of . As explained before, we do not even need that much, the fragment we use to implement it basically fits into . In any paper proof, such a computability result would be immediately brushed off as obvious, barely requiring any explanation. Now, given the non-trivial size of our untyped language, implementing evaluation and proving anything about it in Coq was already quite cumbersome. By contrast, doing the same directly in the object theory is monstruous enough to drive any sane person into sheer madness, not even mentioning that we have to work up to a Gödel encoding. Out of common decency we will not attempt to close this unquestionable gap.
10. Future Work
Although we did not formally prove it out of unrepented sloth, it is quite clear that enjoys decidability of type-checking. Since type interpretation is unchanged in the logical relation, the global shape of the algorithm remains the same as the one for . Handling the quoting primitives should not cause any trouble since their reduction rules enjoy the same kind of properties as in vanilla . Given that our Coq proof is based on a development that proves decidability of type-checking for , it should be quite simple to extend it to .
Another interesting topic is the compatibility of with the full Russian axiomatic. We now know that it is compatible with and in isolation. Hence a natural question is whether it can accommodate both axioms at the same time. We are convinced that not only this is the case, but also that the model described here can be easily extended to handle . The reason for this confidence lies in the uncanny similarity between those two principles. Just like , it is true that Markov’s rule, the external version of , is derivable in using Friedman’s trick.20 Again, like , the return type of this rule is a concrete data type, that is, a formula. It should therefore be easy to add a term
that only computes when both arguments are closed and returns the witness extracted by Friedman’s trick. One must be careful to return the same integer for convertible arguments, but this is easily obtained by returning the smallest index s.t. is 0.
We believe that many axioms can be added to this way, provided they are admissible on closed terms and return formulae that have sufficiently unique inhabitants. We leave the exploration of this subject to a later time.
11. Conclusion
In this paper, we proved that it was possible to add to without disrupting any of the desirable properties of the resulting system such as consistency, strong normalization, and canonicity. Against all odds, the model used for this is the most straightforward one can conceive, as it boils down to the standard logical relation for . The computational content of our variant of Church’s thesis is too borderline stupid to even be considered unsurprising: it computes on closed terms, period. The only mildly non-trivial phenomenon is the need for erasure of annotations and maximal -reduction, but that trick is hardly worthy of attention. As a result, we are still bewildered about the reason for which this problem was believed to be hard.
The theorems have been formalized in Coq, greatly reducing the risk of an accidental error in the proof. For simplicity, the development still axiomatizes the computation model in the object theory. In all likelihood, these axioms would be deemed self-evident in a computability theory paper proof.
Finally, we believe that the generic recipe we followed for this model can be generalized to many other admissible principles in dependent type theory.



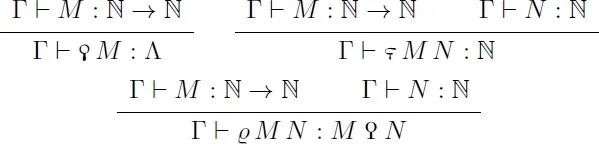
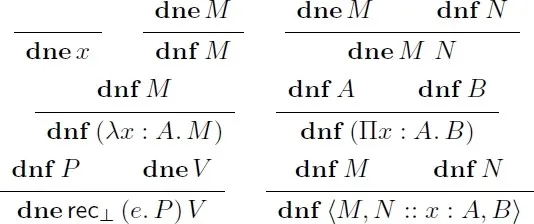

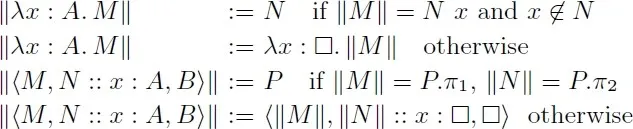

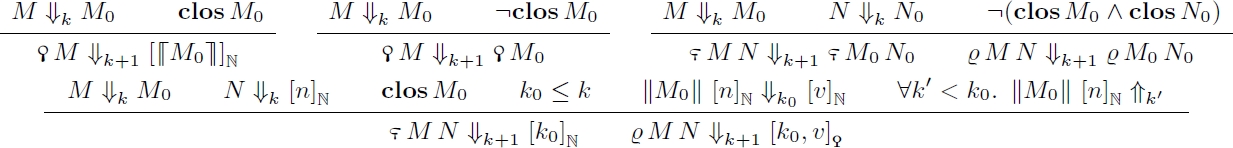





Join the Discussion (0)
Become a Member or Sign In to Post a Comment